Summary:
This article explores the concept of matrix equations in linear algebra. It explains linear combinations and how they relate to matrix equations. It also discusses matrix multiplication and its properties. The article concludes by highlighting the importance of matrix multiplication in neural networks.
Solving Matrix Equations: A Practical AI Solution for Middle Managers
Preface
Welcome to the fourth edition of our series on Linear Algebra, the foundational math behind machine learning. In this article, we’ll explore the matrix equation Ax = b and its connection to solving systems of linear equations.
To get the most out of this article, we recommend reading it alongside the book “Linear Algebra and Its Applications” by David C. Lay, Steven R. Lay, and Judi J. McDonald.
Feel free to share your thoughts and questions with us.
The Intuition
In our previous article, we discussed linear combinations, which have important implications. A vector b is a linear combination of vectors v₁, v₂, …, vₐ in ℝⁿ if there exists a set of weights c₁, c₂, …, cₐ such that c₁v₁ + c₂v₂ + … + cₐvₐ = b.
To determine if b is a linear combination of given vectors v₁, v₂, …, vₐ, we arrange the vectors into a system of linear equations, create an augmented matrix, and use row reduction operations to simplify the matrix. If there is an inconsistency (a row with [0, 0, …, m] where m ≠ 0), then b is not a linear combination. If there is no inconsistency, then b can be written as a linear combination.
This verification process is equivalent to the matrix equation Ax = b!
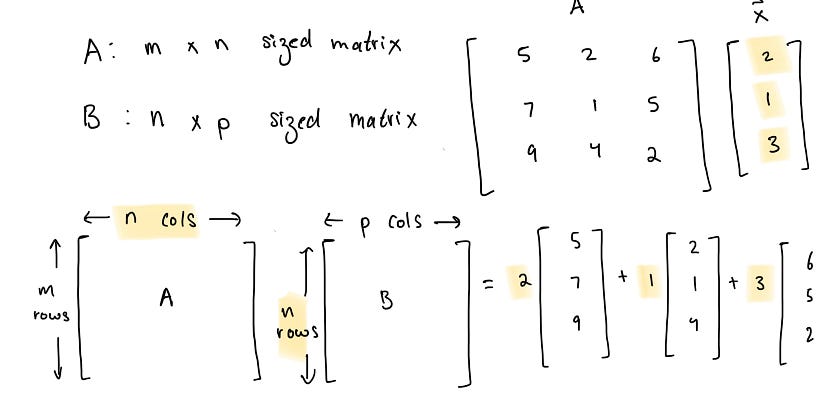
Ax = b
If A is an m x n matrix and x is in Rⁿ, then the product Ax is the linear combination of the vectors (columns) in A, using the corresponding scalars in x.
In other words, if we have an m x n matrix A and a vector x, and we compute the product Ax and it equals b, then b can be written as a linear combination of the columns of A.
Matrix Multiplication
Now that we understand Ax = b, let’s delve into matrix multiplication, which is what Ax actually represents.
Matrix multiplication is the operation of multiplying two matrices to produce their product. In order to perform matrix multiplication, the number of columns in the first matrix (A) must be equal to the number of rows in the second matrix (B).
To compute the product of matrix A and matrix B, we take the dot product of each row in A with each column in B. The resulting matrix C will have m rows (number of rows in A) and p columns (number of columns in B).
Properties of Matrix Multiplication
There are a few important properties to note about matrix multiplication:
– Matrix multiplication is not commutative, meaning AB is not necessarily equal to BA.
– Matrix multiplication is associative: (AB)C = A(BC).
– Matrix multiplication is distributive: A(B+C) = AB + AC and (B+C)A = BA + CA.
– The product of a matrix and the zero matrix is the zero matrix: 0A = 0.
Conclusion
Matrix multiplication is a fundamental operation that plays a crucial role in machine learning, particularly in neural networks. It is used in the feedforward and backpropagation phases of neural network operations.
By understanding matrix equations and matrix multiplication, middle managers can identify automation opportunities, define key performance indicators, select suitable AI solutions, and implement them gradually for measurable business outcomes.
If you want to evolve your company with AI, stay competitive, and redefine your sales processes and customer engagement, consider exploring AI solutions like the AI Sales Bot from itinai.com. It can automate customer engagement, manage interactions across all stages of the customer journey, and provide 24/7 support.
For more information on AI KPI management and continuous insights into leveraging AI, connect with us at hello@itinai.com or follow us on Telegram t.me/itinainews and Twitter @itinaicom.
List of Useful Links:
- AI Lab in Telegram @aiscrumbot – free consultation
- Linear Algebra 4: Matrix Equations
- Towards Data Science – Medium
- Twitter – @itinaicom

























