Understanding Neural Ordinary Differential Equations (ODEs)
Neural Ordinary Differential Equations (ODEs) are crucial for scientific modeling and analyzing time-series data that changes frequently. Unlike traditional neural networks, this framework uses differential equations to model continuous-time dynamics.
Challenges with Neural ODEs
While Neural ODEs effectively manage dynamic data, calculating gradients for backpropagation remains a challenge, limiting their usefulness. The common approach, recursive checkpointing, balances memory and computation but often leads to inefficiencies, increasing both memory usage and processing time.
Innovative Solutions from the University of Bath
Researchers at the University of Bath have developed a new machine learning framework to improve backpropagation in Neural ODE solvers. They introduced a class of algebraically reversible solvers that reconstruct the solver state at any time without needing to store intermediate calculations. This innovation significantly enhances efficiency by reducing memory usage and computational demands.
Key Advantages of the New Solver
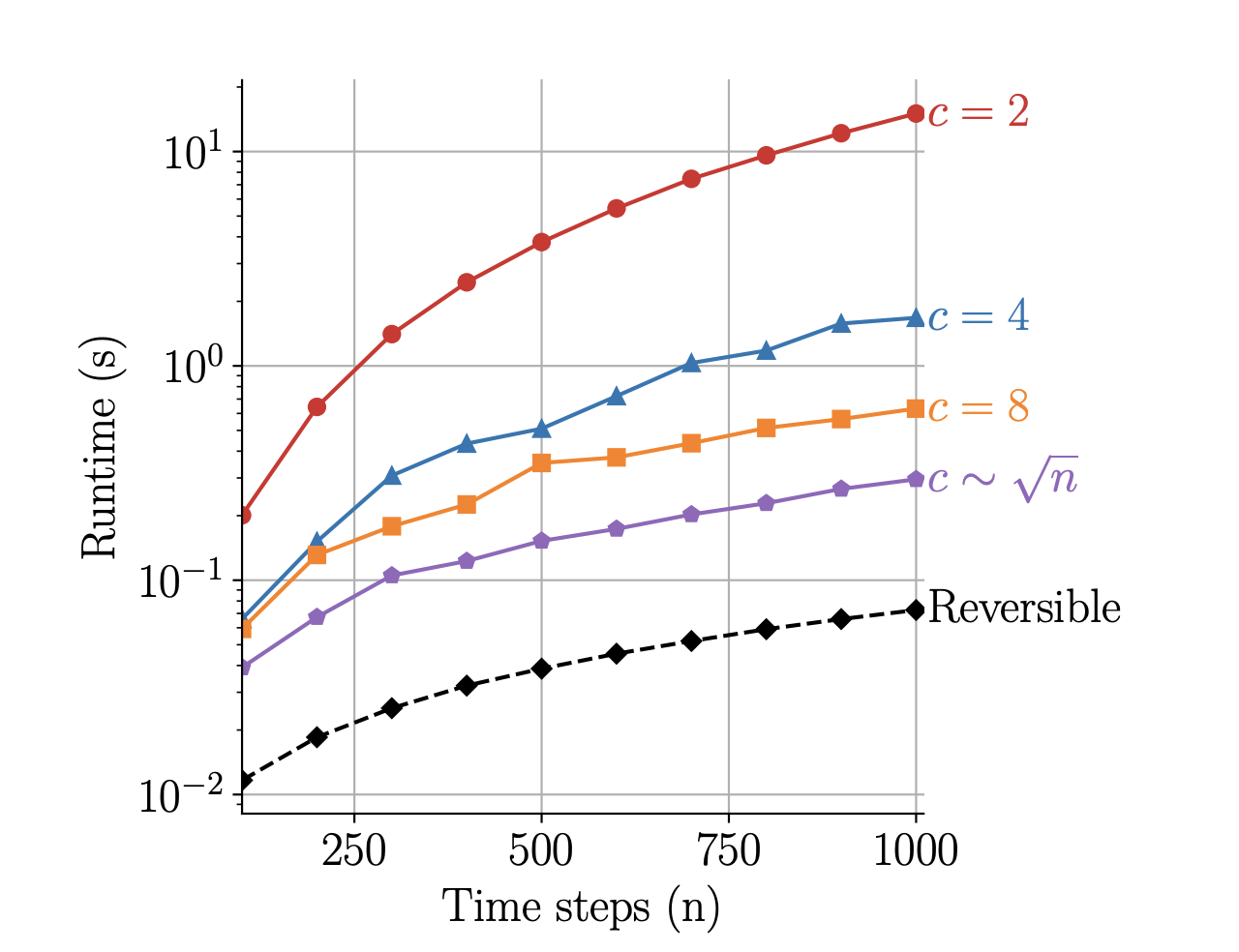
- Operation complexity of O(n) and memory usage of O(1).
- Allows any single-step numerical solver to be reversible, ensuring exact gradient calculations.
- Improves numerical stability and convergence rates.
How It Works
Instead of saving every state during the forward pass, the algorithm reconstructs these states in reverse during the backward pass. A coupling parameter, λ, helps maintain stability while tracing the computational path accurately. This method retains essential information compactly, allowing for precise gradient calculations without traditional storage overhead.
Experimental Validation
The research team conducted experiments to compare the new solvers with traditional recursive checkpointing methods. They tested:
- Data discovery from Chandrasekhar’s White Dwarf Equation.
- Dynamics approximation from a coupled oscillator system.
- Chaotic dynamics identification using a chaotic double pendulum dataset.
The results showed that the new solvers were up to 2.9 times faster and used up to 22 times less memory than conventional methods, while maintaining accuracy.
Conclusion
This research introduces a new class of algebraic solvers that enhance computational efficiency and gradient accuracy, paving the way for scalable and robust models in time series and dynamic data analysis.
Explore Further
Check out the Paper for more details. Follow us on Twitter, join our Telegram Channel, and connect with our LinkedIn Group. Join our community of over 75k+ ML enthusiasts on Reddit.
Transform Your Business with AI
Stay competitive by leveraging the efficient machine learning methods developed by the University of Bath. Here’s how AI can transform your operations:
- Identify Automation Opportunities: Find key areas in customer interactions that can benefit from AI.
- Define KPIs: Ensure your AI initiatives have measurable impacts on your business.
- Select an AI Solution: Choose tools that fit your needs and allow for customization.
- Implement Gradually: Start with a pilot project, gather data, and expand AI usage wisely.
For AI KPI management advice, contact us at hello@itinai.com. For ongoing insights into AI, follow us on Telegram or Twitter.
Enhance Your Sales and Customer Engagement
Discover how AI can redefine your sales processes and customer engagement. Explore solutions at itinai.com.




























