Importance of Sampling from Complex Probability Distributions
Sampling from complex probability distributions is crucial in fields like statistical modeling, machine learning, and physics. It helps generate representative data points to solve problems such as:
- Bayesian inference
- Molecular simulations
- High-dimensional optimization
Sampling requires algorithms to explore high-probability areas of a distribution, which can be challenging, especially in high dimensions.
Challenges in Sampling
One major challenge is sampling from unnormalized densities, where the normalizing constant is often unavailable. This makes evaluating the likelihood of points difficult. As dimensionality increases, traditional methods become inefficient, struggling to balance computational efficiency and sampling accuracy.
Current Approaches and Their Limitations
- Sequential Monte Carlo (SMC): Gradually evolves particles toward a target distribution but can converge slowly due to predefined transitions.
- Diffusion-based Methods: Learn dynamics to transport samples but may face instability and mode collapse during training.
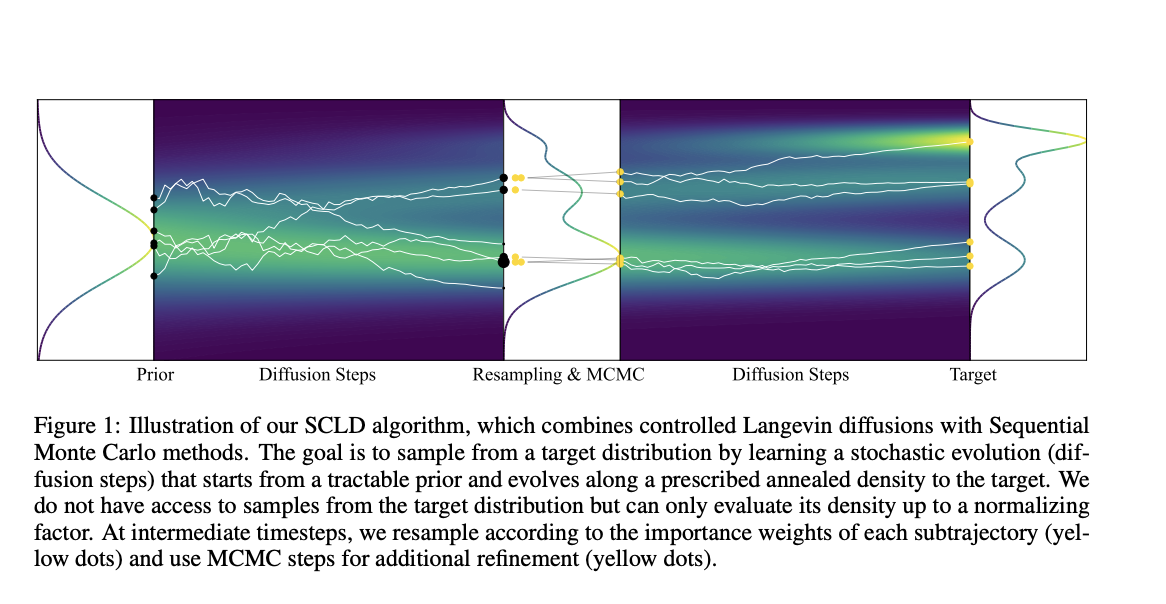
Introducing Sequential Controlled Langevin Diffusion (SCLD)
A team of researchers developed a new method called SCLD, combining the strengths of SMC and diffusion-based methods. This approach allows for:
- Seamless integration of learned transitions with SMC resampling.
- Optimization of particle trajectories using adaptive controls.
- End-to-end optimization for improved performance.
Key Features of SCLD
SCLD uses a log-variance loss function for numerical stability and scales well in high dimensions. It effectively explores complex distributions without getting stuck in local optima.
Performance and Results
The SCLD algorithm was tested on 11 benchmark tasks, including:
- High-dimensional Gaussian mixture models
- Robotic arm configurations
- Bayesian inference for credit datasets
SCLD outperformed traditional methods, achieving top results with only 10% of the training budget required by other diffusion methods.
Key Insights
- The hybrid approach balances robustness and flexibility for efficient sampling.
- SCLD achieves high accuracy with minimal resources, often needing only 10% of the training iterations of competitors.
- It performs well in high-dimensional tasks, avoiding common issues like mode collapse.
- The method is versatile, applicable in robotics, Bayesian inference, and molecular simulations.
Conclusion
The SCLD algorithm effectively addresses the limitations of existing sampling methods, providing greater efficiency and accuracy with minimal resources. It sets a new benchmark for sampling algorithms in complex statistical computations.
Get Involved
Check out the research paper for more details. Follow us on Twitter, join our Telegram Channel, and connect with our LinkedIn Group. Don’t forget to join our 60k+ ML SubReddit.
Transform Your Business with AI
Stay competitive by leveraging AI solutions. Here’s how:
- Identify Automation Opportunities: Find key customer interaction points that can benefit from AI.
- Define KPIs: Ensure measurable impacts on business outcomes.
- Select an AI Solution: Choose tools that meet your needs and allow customization.
- Implement Gradually: Start with a pilot, gather data, and expand AI usage wisely.
For AI KPI management advice, connect with us at hello@itinai.com. For continuous insights, follow us on Telegram or Twitter @itinaicom.
Discover how AI can enhance your sales processes and customer engagement at itinai.com.


























