Mathematical Reasoning in AI: A Game Changer
Revolutionizing Problem-Solving
AI is transforming fields like science and engineering by enhancing machines’ ability to tackle complex logical challenges. Despite recent advancements, solving intricate mathematical problems, particularly at Olympiad levels, remains difficult. This drives ongoing research to improve AI’s accuracy and reliability in mathematical reasoning.
Challenges in AI Reasoning
A significant hurdle is creating precise step-by-step solutions for complex problems. Traditional methods often struggle, especially with multi-step questions that require consistent logical flow. Current techniques, like Chain-of-Thought (CoT), can lead to errors and inefficiencies, highlighting the need for innovative approaches.
Emerging Solutions
New strategies like Monte Carlo Tree Search (MCTS), Tree-of-Thought (ToT), and Breadth-First Search (BFS) aim to improve AI reasoning. However, these methods can get trapped in suboptimal solutions, limiting their effectiveness in vast mathematical solution spaces.
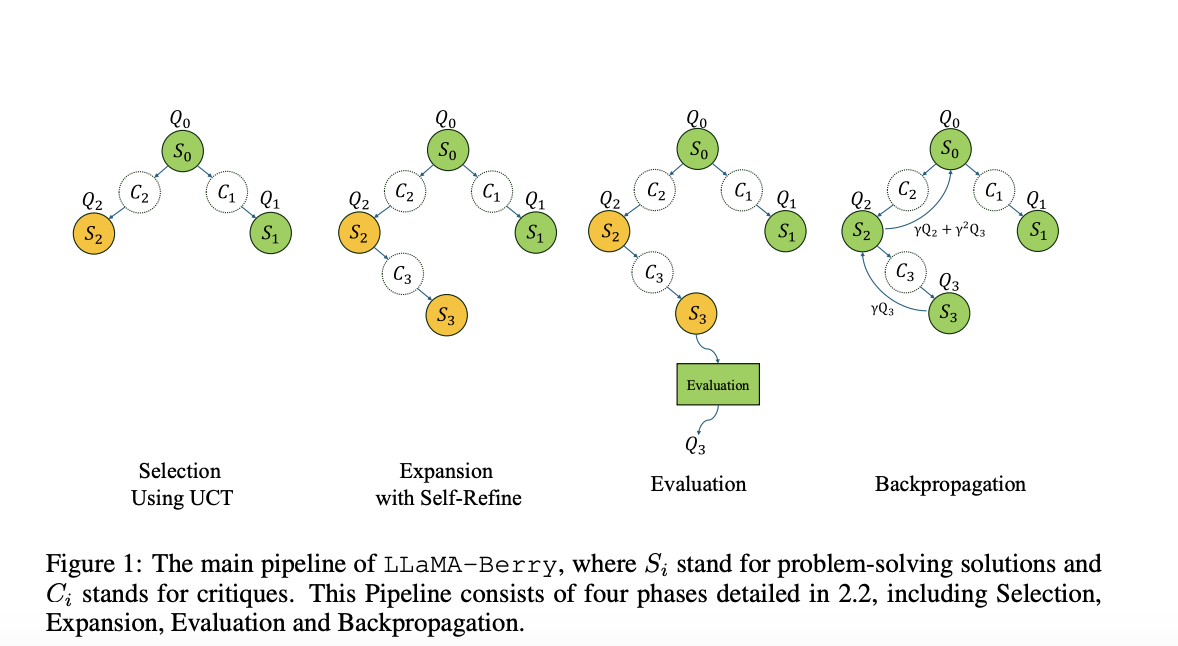
Introducing LLaMA-Berry
A collaborative research team from leading universities has developed LLaMA-Berry, a groundbreaking framework that combines MCTS with a Self-Refine (SR) optimization technique. This system enhances the exploration of reasoning paths and utilizes the Pairwise Preference Reward Model (PPRM) for dynamic evaluation of solutions.
How LLaMA-Berry Works
LLaMA-Berry’s Self-Refine method treats each solution as a complete entity, enhancing the reasoning process through iterative refinements. Its structured phases—Selection, Expansion, Evaluation, and Backpropagation—ensure a balanced exploration of solutions. The PPRM assesses solutions comparatively, which prevents overcommitment to flawed paths.
Success in Testing
Testing has shown that LLaMA-Berry surpasses existing models in solving complicated Olympiad-level problems. For example, it achieved over an 11% performance boost on the AIME24 benchmark, reaching an impressive accuracy of 55.1% in challenging mathematics tasks, demonstrating its effectiveness without needing extensive training.
Key Takeaways from LLaMA-Berry Research
– **Benchmark Success:** Achieved up to 96.1% accuracy on GSM8K and 55.1% on Olympiad-level tasks.
– **Comparative Evaluation:** Enhanced evaluation with PPRM provides a balanced view of solution preferences.
– **Optimized Solution Paths:** Self-Refine and MCTS work together to enhance reasoning efficiency.
– **Resource Efficiency:** Outperformed competitors using fewer resources, achieving significant improvements.
– **Scalability and Adaptability:** Potential to expand beyond mathematics to other complex reasoning tasks in science and engineering.
Conclusion
LLaMA-Berry marks a significant leap in AI’s ability to handle complex mathematical reasoning effectively. By combining Self-Refine, MCTS, and PPRM, it outperforms traditional models on tough benchmarks. This innovative approach positions LLaMA-Berry as a valuable tool for high-stakes AI applications, with the potential to adapt to other challenging fields like physics and engineering.
Stay Connected
Check out the Paper and GitHub Page for more insights. Follow us on Twitter, join our Telegram Channel, and connect with our LinkedIn Group. If you appreciate our work, subscribe to our newsletter and join our thriving ML SubReddit community of over 55k members.
Explore AI Solutions for Your Business
Evolve your company with LLaMA-Berry and discover how AI can transform your operations.
– **Identify Automation Opportunities:** Find key areas for AI enhancements.
– **Define KPIs:** Measure the impact of your AI initiatives.
– **Select the Right Solution:** Choose customizable tools that fit your needs.
– **Implement Gradually:** Pilot projects, gather data, and expand wisely.
For AI KPI management advice, contact us at hello@itinai.com. For ongoing insights, follow us on Telegram and Twitter.



























