This article discusses vector equations and spans in linear algebra. It explains the concept of vectors in different dimensions and their geometric visualization. Additionally, it covers the algebraic properties of vectors, linear combinations, and the span of a set of vectors. These fundamental concepts help understand the structure of vector spaces and their relationships.
Linear Algebra 3: Vector Equations
Vectors and Spans
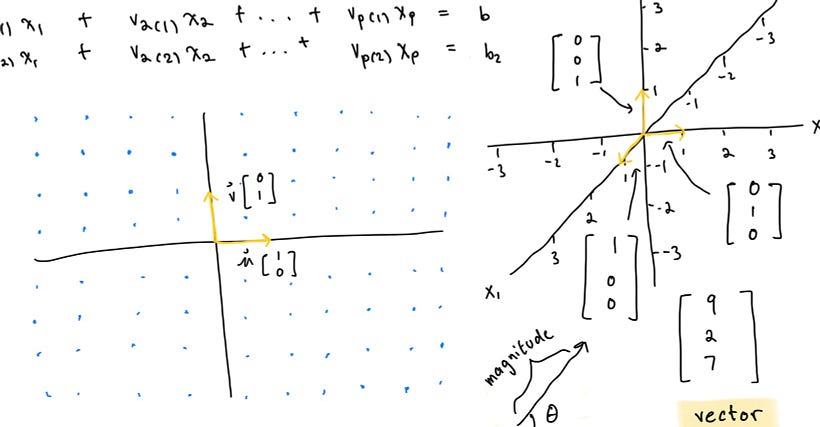
In this article, we explore the basics of Linear Algebra, focusing on vectors and spans. Vectors are special kinds of matrices with a size of m x 1, where m represents the number of entries in the vector. Vectors can exist in different dimensions, such as ℝ², ℝ³, ℝⁿ, depending on the number of entries. The zero vector, where all entries are zero, is also an important concept. Vectors can be graphically visualized, helping us understand their magnitude and direction.
Algebraic Properties of Vectors
Vectors have certain algebraic properties that hold true for all vectors and scalars. These properties include commutativity, associativity, additive identity, additive inverse, and distributivity with vectors and scalars. These properties are tied to vector addition and scalar multiplication.
Linear Combinations
Linear combinations involve combining vectors using scalar multiples. Given a set of vectors v₁, v₂, …, vₐ and corresponding weights c₁, c₂, …, cₐ, the linear combination is the vector defined by the sum of the scalar multiples. Linear combinations are connected to the existence problem in Linear Algebra and can be used to determine if a vector is a linear combination of a set of vectors.
Span of a Set of Vectors
The span of a set of vectors refers to the set of all possible linear combinations of those vectors. It is denoted as Span{v₁, v₂, …, vₐ}. The span contains all the vectors that can be written as a linear combination of the given vectors. The span can be visualized and helps us understand the range of vectors that can be reached using linear combinations.
Conclusion
Understanding vectors, linear combinations, and spans is crucial in the field of Linear Algebra. These concepts help us grasp the structure of vector spaces and the relationships between different sets of vectors. They are connected to other core concepts in Linear Algebra, such as the existence of solutions and row echelon forms. By leveraging these concepts, companies can evolve and stay competitive with the help of AI solutions.
For more information on how AI can transform your company, contact us at hello@itinai.com. Visit itinai.com/aisalesbot to explore our AI Sales Bot, designed to automate customer engagement and streamline sales processes. Stay updated on AI insights by following us on Telegram at t.me/itinainews or Twitter @itinaicom.
