This article discusses the combination of quantum computing properties with a classic Machine Learning technique called Support Vector Machine (SVM). The author explores the concept of SVM, the use of kernels for classification, and introduces quantum kernels. An example using Pennylane and scikit-learn’s SVC is provided, showing that the performance of a quantum kernel didn’t outperform an SVM with a radial basis function (RBF) kernel. The author mentions the need for careful design when using quantum kernels.
Rephrased text:
Combining Quantum Computing Properties with Machine Learning
Introduction
Quantum Machine Learning (QML) is a promising field that utilizes the probabilistic nature of quantum systems to develop models. While quantum computers are not yet widely accessible, data scientists are exploring how to leverage the quantum paradigm to create scalable models. The growth in this area is accelerating, although it is difficult to predict exactly when quantum hardware will be advanced enough for practical use.
In my recent studies, I focused on designing Variational Quantum Classifiers (VQCs), as detailed in a previous post. This is an interesting case to study for beginners in QML.
However, I also wanted to explore a quantum approach to the Support Vector Machine (SVM) and understand how it could be translated into the quantum world.
Initially, I had a biased perspective from studying VQCs and tried to imagine how SVM could be translated into a parameterizable quantum circuit. However, I discovered that the quantum enhancement works differently, which was a pleasant surprise that expanded my understanding of the subject.
In this post, I provide a brief introduction to SVM, explain how to apply a Quantum Machine Learning (QML) approach to this technique, and demonstrate an example of a quantum-enhanced SVM (QSVM) using the Titanic dataset.
SVM and Kernels
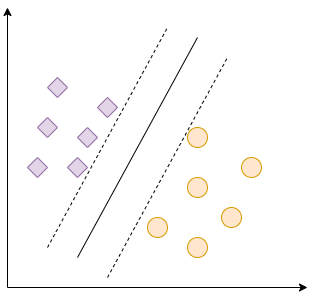
SVM, specifically the Support Vector Classifier (SVC), is used for classification problems. Its objective is to find a hyperplane that effectively separates data from different classes with the largest margin. Initially, this may not seem very useful.
The hyperplane is the line that separates the classes. In a two-dimensional vector space, if we have two classes, we can draw a line that separates them. The solid line represents the hyperplane that provides the best possible margin, as indicated by the dashed lines. The goal of SVM is to find this optimal separator.
In the above example, we used a simple linear hyperplane. However, in cases where the data is not linearly separable, such as in the second example, SVM cannot directly solve the problem. To address this, a technique called kernel trick is used.
The kernel trick involves transforming the data into a higher-dimensional space, such as in the equation shown. In this higher-dimensional space, we can draw a plane that separates the two classes optimally. This is depicted in Figure 3.
In SVM, the function f that performs this transformation is known as the kernel. It projects the data into a higher-dimensional space, making it easier to find a hyperplane that can accurately identify data from different classes.
There are various kernels available to solve different problems. One popular option is the Radial Basis Function (RBF) kernel, which is the default kernel in scikit-learn’s SVC. This kernel is not described by an analytic function, but rather by a similarity matrix based on the kernel.
However, if we want to be more creative, we can explore the quantum approach. Quantum computing offers an exponential relation between qubits and quantum states, making it an interesting option for designing powerful kernels. The quantum system can drive our data towards a high-dimensional vector space, depending on the number of qubits used.
Quantum Kernels
Quantum kernels are usually defined by a similarity matrix based on a quantum circuit, which may or may not be parameterizable. Both Pennylane and Qiskit offer built-in functions to create kernels that can be used in scikit-learn’s SVC.
The process of creating a quantum kernel involves:
1. Embedding data into quantum states
2. Designing a quantum circuit that could potentially be parameterizable
3. Working with superposition and entanglement between states to obtain the best results
After the quantum circuit is designed, it is used to build a similarity matrix.
Example
In this example, we demonstrate a simple quantum kernel using Pennylane. We apply this kernel to the Titanic Classification dataset, where the goal is to predict whether a person survived the Titanic tragedy based on variables like age, gender, and boarding class.
We create a quantum kernel using the Basis Embedding method, which embeds our data into quantum states. We apply Hadamard gates to introduce superposition and CNOT gates to generate entanglement between our qubits. The resulting quantum circuit generates superposition and entanglement among the variables.
Our quantum kernel is then used in an SVC from scikit-learn to train and test the model. The results show that the SVC with the RBF kernel performs better than the SVC with the quantum kernel. The quantum approach had good precision but lower recall, indicating a significant number of false negatives.
Conclusion
Quantum kernels have the potential to enhance SVM performance. However, as demonstrated in our example, a simple quantum kernel may not outperform the classical RBF kernel. Designing parameterizable quantum kernels requires careful consideration to be competitive with classical techniques. Further research is being conducted in this area.
For more information on SVMs with quantum kernels, we recommend reading the referenced posts and texts.
Action Items:
1. Research quantum machine learning (QML) and its applications in developing scalable models. Look for resources and articles that discuss the latest advancements and techniques in this field.
2. Study Variational Quantum Classifiers (VQCs) and understand how they differ from traditional SVM approaches. Consider how quantum enhancement can be applied to SVM.
3. Explore quantum kernels and their use in quantum circuits. Investigate the parameterizable and non-parameterizable options available in Pennylane and Qiskit.
4. Familiarize yourself with the Titanic Classification dataset and its variables. Understand how to preprocess the data and prepare it for quantum embedding.
5. Implement a simple quantum kernel using Pennylane and apply it to an SVC from scikit-learn. Ensure that the kernel generates superposition and entanglement between the variables.
6. Compare the performance of the quantum kernel SVM with a traditional RBF kernel SVM. Analyze the results in terms of accuracy, precision, recall, and F1 score.
7. Continue researching and exploring parameterizable quantum kernels. Stay updated on new developments and techniques in the field.
8. Document your findings and share any interesting insights or progress made in designing parameterizable quantum kernels.
