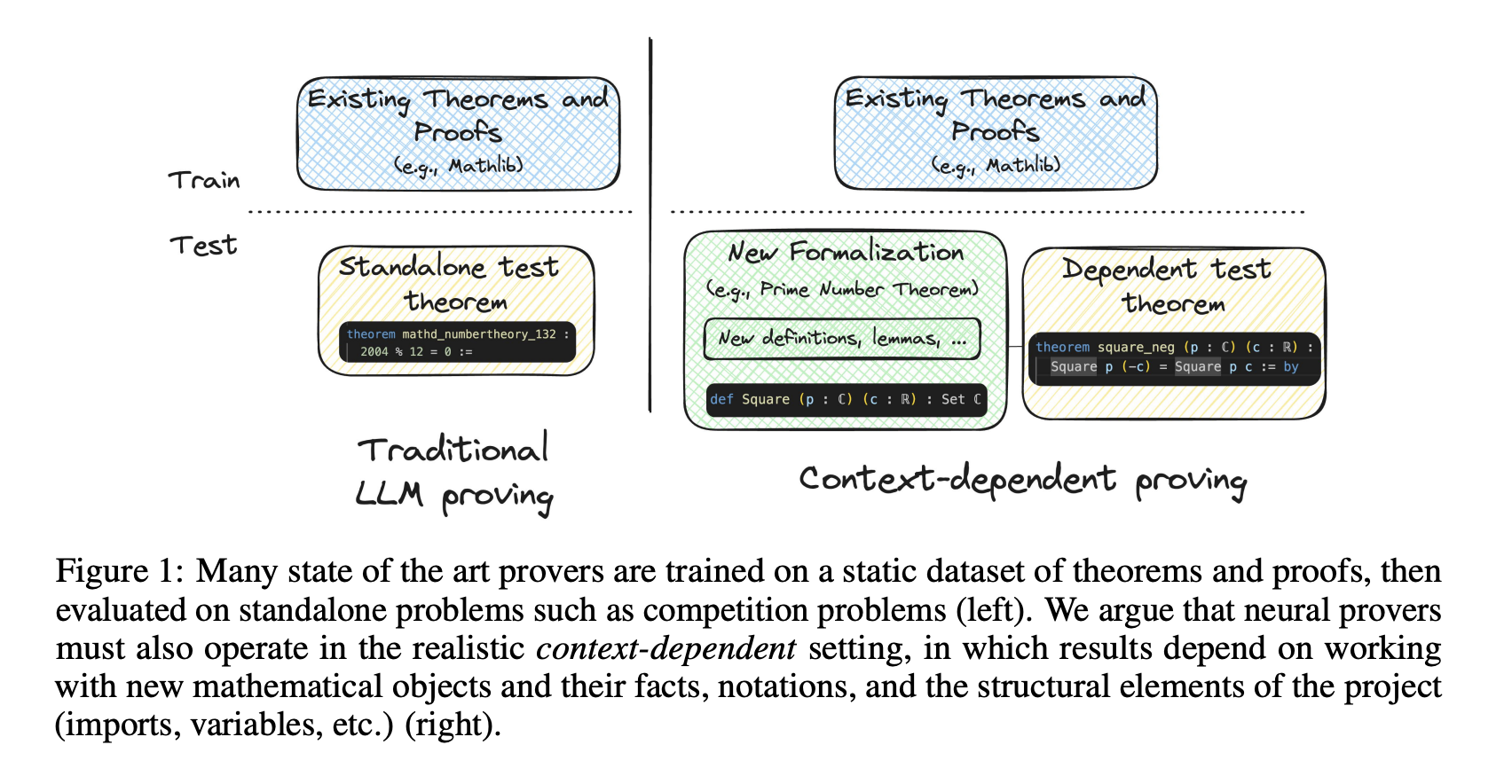
Understanding Formal Theorem Proving and Its Importance
Formal theorem proving is essential for evaluating the reasoning skills of large language models (LLMs). It plays a crucial role in automating mathematical tasks. While LLMs can assist mathematicians with proof completion and formalization, there is a significant challenge in aligning evaluation methods with real-world theorem proving complexities.
Challenges in Current Evaluation Methods
Current evaluation methods often do not reflect the intricate nature of mathematical reasoning needed for real theorem proving. This gap raises concerns about the effectiveness of LLM-based provers in practical applications. There is a clear need for advanced evaluation frameworks that can accurately assess an LLM’s capabilities in tackling complex mathematical proofs.
Innovative Approaches to Enhance Theorem-Proving Capabilities
Several methods have been developed to improve the theorem-proving abilities of language models:
- Next Tactic Prediction: Models predict the next proof step based on the current state.
- Premise Retrieval Conditioning: Relevant mathematical premises are included in the generation process.
- Informal Proof Conditioning: Natural language proofs guide the model’s output.
- File Context Fine-Tuning: Models generate complete proofs without needing intermediate steps.
While these methods have shown improvements, they often focus on specific aspects rather than the full complexity of theorem proving.
Introducing MiniCTX: A New Benchmark System
Researchers at Carnegie Mellon University have developed MiniCTX, a groundbreaking benchmark system aimed at enhancing the evaluation of theorem-proving capabilities in LLMs. This system offers a comprehensive approach by integrating various contextual elements that previous methods overlooked.
Key Features of MiniCTX
- Comprehensive Context Handling: MiniCTX incorporates premises, prior proofs, comments, notation, and structural components.
- NTP-TOOLKIT Support: An automated tool that extracts relevant theorems and contexts from Lean projects, ensuring up-to-date information.
- Robust Dataset: The system includes 376 theorems from diverse mathematical projects, allowing for realistic evaluations.
Performance Improvements with Context-Dependent Methods
Experimental results show significant performance gains when using context-dependent methods. For example:
- The file-tuned model achieved a 35.94% success rate compared to 19.53% for the state-tactic model.
- Providing preceding file context to GPT-4o improved its success rate to 27.08% from 11.72%.
These results highlight the effectiveness of MiniCTX in evaluating context-dependent proving capabilities.
Future Directions for Theorem Proving
Research indicates several areas for improvement in context-dependent theorem proving:
- Handling long contexts effectively without losing valuable information.
- Integrating repository-level context and cross-file dependencies.
- Improving performance on complex proofs that require extensive reasoning.
Get Involved and Stay Updated
Explore the Paper and Project for more insights. Follow us on Twitter, join our Telegram Channel, and connect with our LinkedIn Group. If you appreciate our work, subscribe to our newsletter and join our 55k+ ML SubReddit.
Upcoming Live Webinar
Oct 29, 2024: Discover the best platform for serving fine-tuned models with the Predibase Inference Engine.
Transform Your Business with AI
Stay competitive by leveraging MiniCTX for advanced theorem proving. Here’s how AI can redefine your work:
- Identify Automation Opportunities: Find key areas for AI integration.
- Define KPIs: Ensure measurable impacts on business outcomes.
- Select an AI Solution: Choose tools that fit your needs.
- Implement Gradually: Start small, gather data, and expand wisely.
For AI KPI management advice, contact us at hello@itinai.com. For ongoing insights, follow us on Telegram or Twitter.
Explore AI Solutions for Sales and Customer Engagement
Discover how AI can enhance your sales processes and customer interactions at itinai.com.

























